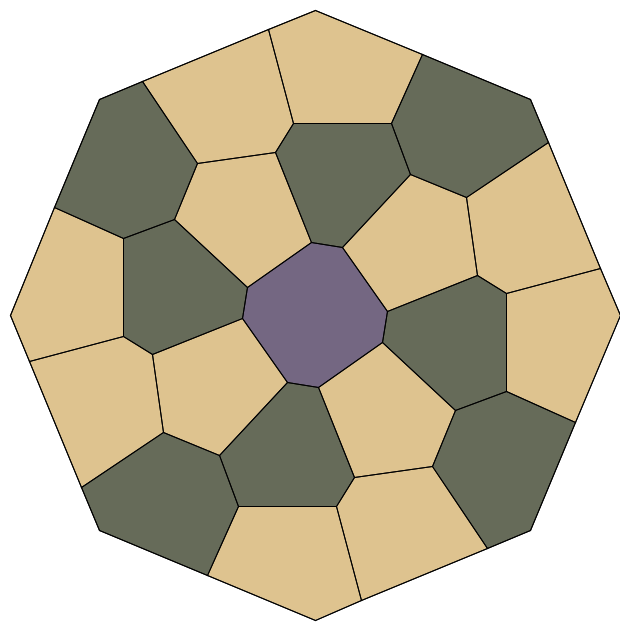

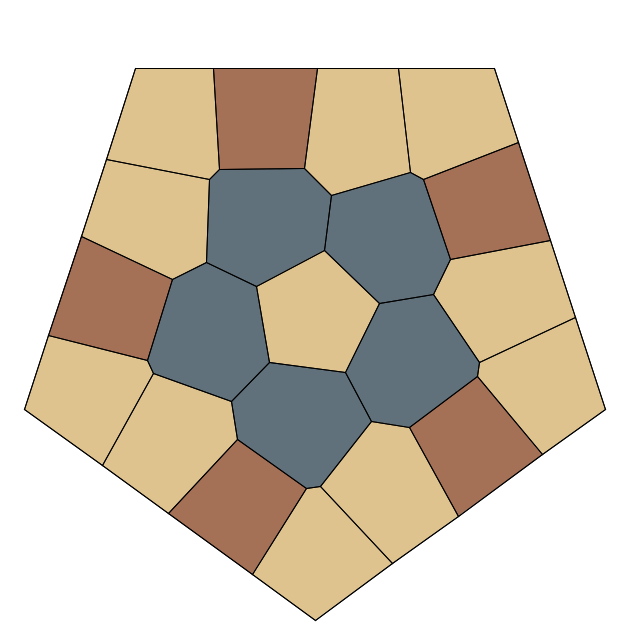

Symmetry in mathematics, can be defined as a mapping from a mathematical object to itself that preserves the object's structure. Its importance lies in its ability to connect math to other disciplines, simplify problem solving and even inspire creativity. Rosettes are remarkable for their tendency, under Lloyd’s relaxation, to settle into symmetric configurations. This symmetry arises naturally—guided by their regular boundaries—and is described mathematically by the two-dimensional point groups, or rosette groups, from which they take their name.
A point group, in mathematical terms, is a set of geometric transformations, including rotations and reflections, that preserve a fixed point. In two dimensions, these groups come in two forms: cyclic groups, consisting solely of rotations, and dihedral groups, which combine rotations with reflections. These so-called rosette groups are commonly denoted by their rotation order 𝑛—the number of distinct rotations. Cyclic groups are designated as Cn, while dihedral groups are represented as Dn. Note that under this notation, cyclic groups contain 𝑛 symmetry operations whereas dihedral groups contains 2𝑛 symmetry operations, due to the inclusion of reflections. Importantly, a configuration described informally as "asymmetric" still mathematically corresponds to the simplest cyclic group, C1, which includes only the trivial symmetry operation—the identity transformation.





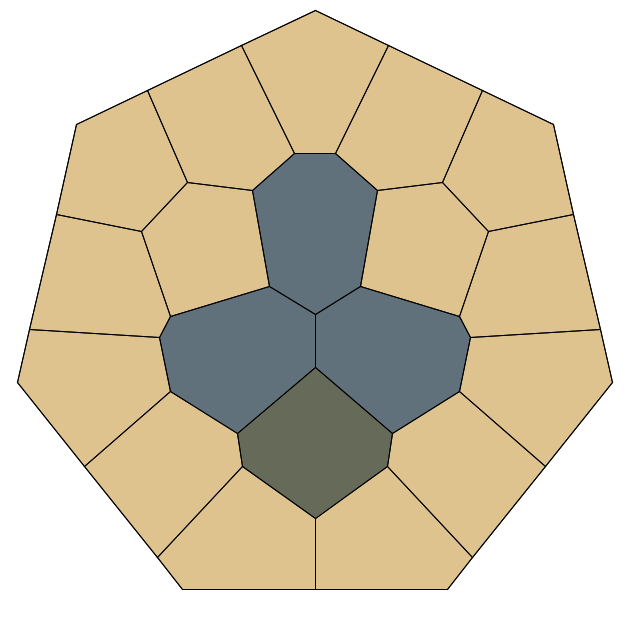

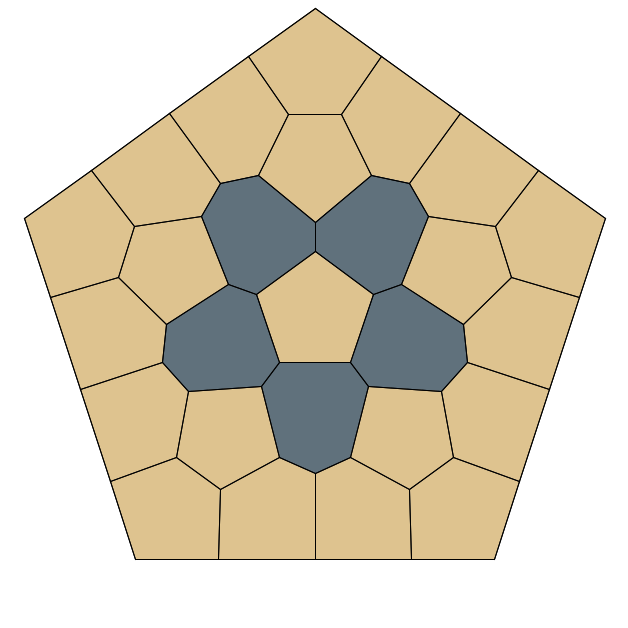

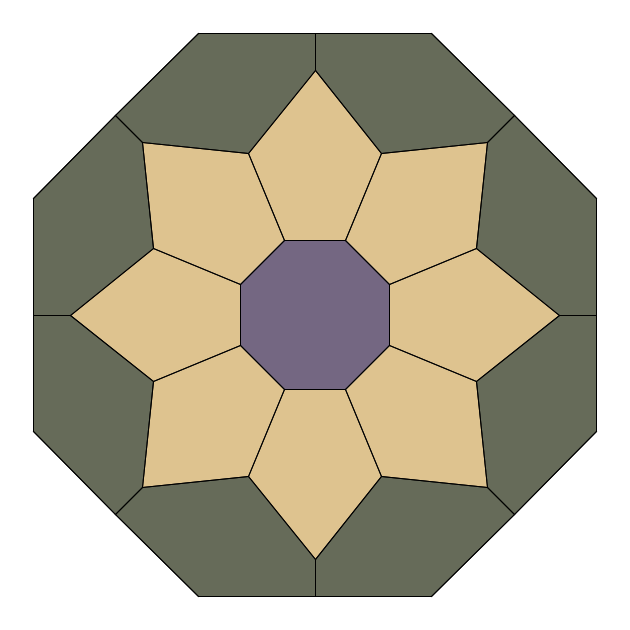

Now that you've seen how Rosettes emerge and evolve, it's time to explore them firsthand. Browse the Rosette Gallery to admire finished designs, or open the Rosette Studio to create your own, tweak the parameters, and watch new patterns unfold before your eyes.