 \(\cap\)
=
\(\cap\)
=
A Rosette is a planar centroidal Voronoi diagram whose boundary is a regular convex polygon. But what exactly does that mean? To unpack this definition, we first need to understand Voronoi diagrams themselves.
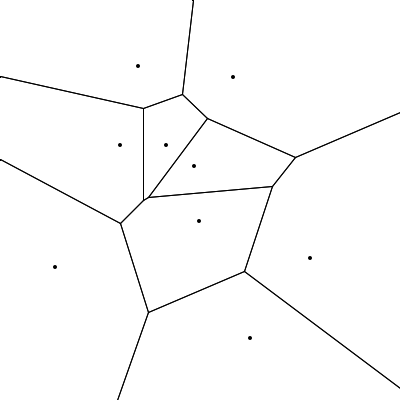
A Voronoi diagram is a partitioning of a metric space, often the Euclidean plane (\(\mathbb{R}^2\)), into regions such that the points in the interior of each region are all closest to one of a number of points called sites or generators
$$\mathcal{P} = \{p_1, p_2, \dots, p_n\} \subset \mathbb{R}^2.$$
Each site \(p_i\) is associated with the region defined by
$$V(p_i) = \{ x \in \mathbb{R}^2 : \|x - p_i\| \le \|x - p_j\| \text{ for every } j \neq i \}.$$
In this construction, the plane is divided so that every point in \(V(p_i)\) is at least as close to \(p_i\) as to any other site. Points equally close to 2 (or more) sites form the edges of the diagram; points equally close to 3 or more sites form the vertices of the diagram.
The regions of the diagram, also known as Voronoi cells, comprise both convex polygons and unbounded polytopes, collectively covering the entire plane.
Voronoi diagrams can be constructed using several approaches. A highly efficient method and the one used to construct Rosettes is Fortune’s algorithm. This algorithm employs a sweep-line technique that tracks a dynamic front called the beachline. As the sweep line moves across the plane, intersections of parabolic arcs along the beachline determine the evolving boundaries of the regions. The algorithm progresses by processing events (sites and circles) in order. Each site event corresponds to the appearance of a new arc on the beachline and a new edge in the diagram. Vertices in the diagram correspond to the disappearance of an arc on the beachline. This happens during a circle event—when two breakpoints converge—their corresponding edges intersecting to form the new vertex (and a new edge).
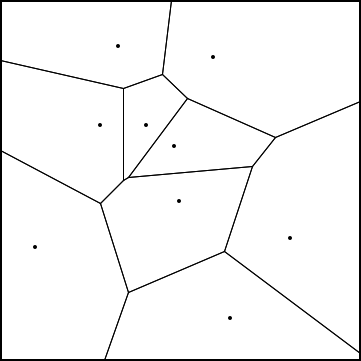
Often, it is useful to examine Voronoi diagrams within a bounded and compact domain \(\Omega \subset \mathbb{R}^2\). Here, each Voronoi cell is defined as
$$V_\Omega(p_i) = V(p_i) \cap \Omega.$$
In practice, these bounded Voronoi diagrams are derived from their unbounded counterparts by intersecting each Voronoi cell with the domain \(\Omega\). This bounded construction not only makes the diagram more suitable for computational purposes but also sets the stage for forming Rosettes, where domains are restricted to regular convex polygons.
 \(\cap\)
=
\(\cap\)
=

Bounded Voronoi diagrams form the coarse geometric structure of Rosettes but Rosettes are more than just geometry. Next, we'll explore how optimization and centroidal Voronoi Diagrams play a role in their formation.